The laws involving exponents are used in everyday scientific applications and are necessary in understanding the natural phenomena that occurs in the real world. For example, in Port au Prince, Haiti, an earthquake of a magnitude of 7.0 on the Richter scale caused a massive amount of devastation. The Richter scale is quantifies the amount of seismic energy that is released by an earthquake, and is measured with a logarithmic base of 10. The earthquake in Haiti therefore had a reading of 10⁷ (with the exponent denoting the amplitude of the earthquake). An earthquake with a reading of 8.0 has an amplitude 10 times greater than that of the earthquake that occurred in Haiti.
The pH scale is another application of the concept of exponents, which measures how acidic or basic a substance is (pH tests are regularly performed in public swimming pools to maintain a pH between 7.0-7.4 to ensure ideal comfort levels for the public as well as effective chlorine action). A substance with a reading of 8.0 is 10 times more alkaline than that of a substance with 8.0; and a substance with a reading of 9.0 is 100 times more alkaline than of a substance with a neutral (7.0) pH.
There are a wide variety of applications of exponents in the natural and scientific world, as well as practical applications, which include the calculation of a monthly mortgage repayments plans for a loan.
BBC. (2010). History of deadly earthquakes. Retrieved on February 21, 2010 from http://news.bbc.co.uk/2/hi/2059330.stm
skip to main |
skip to sidebar
.jpg)
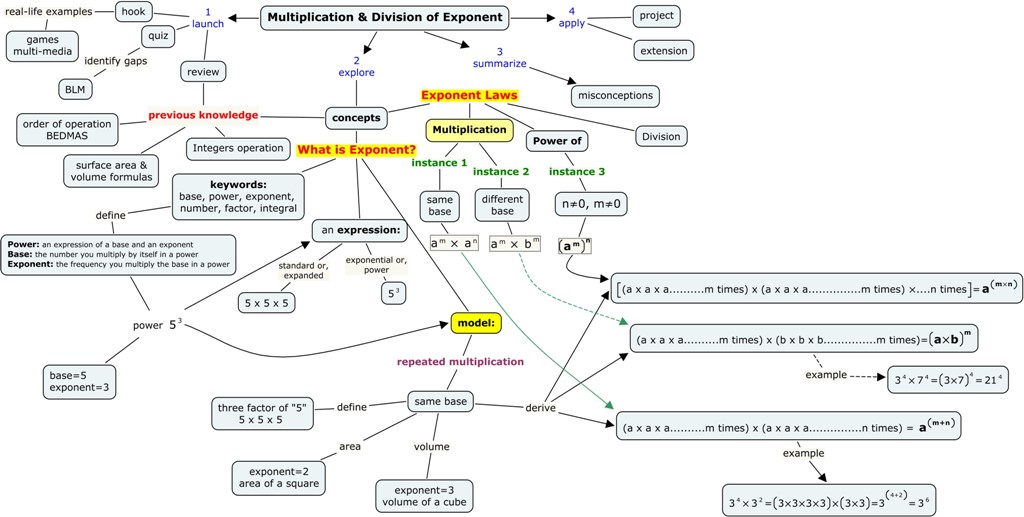
A concept-map of multiplication of exponents
This is a series of activities that can help deepen student understanding of exponents. What exactly is exponents? Which grade levels would these materials pertain to?
Our Goal
"Understanding Multiplication of Exponents"
To create an instructional sequence (a.k.a. lesson plan) featuring:- different models to present the concept- select problems to facilitate student understanding- explanations to bring about student understanding- common student misconceptions- ways to address misconceptions- connections to real world experiences- connections among mathematical ideas
Lesson Plan for Junior-High School Exponents
.jpg)
A concept-map of multiplication of exponents
About this Blog
We are student teachers at the University of Calgary, Alberta, Canada. As future educators majoring in secondary Math, we are posting this blog to share our views on how we would attempt to explain exponents to junior high students. Our target audience is anyone seeking a deeper understanding of exponents and concepts of multiplication of exponents at the school grade level 9.