Basic of Exponent Multiplication

Model 1: Repeated Multiplication

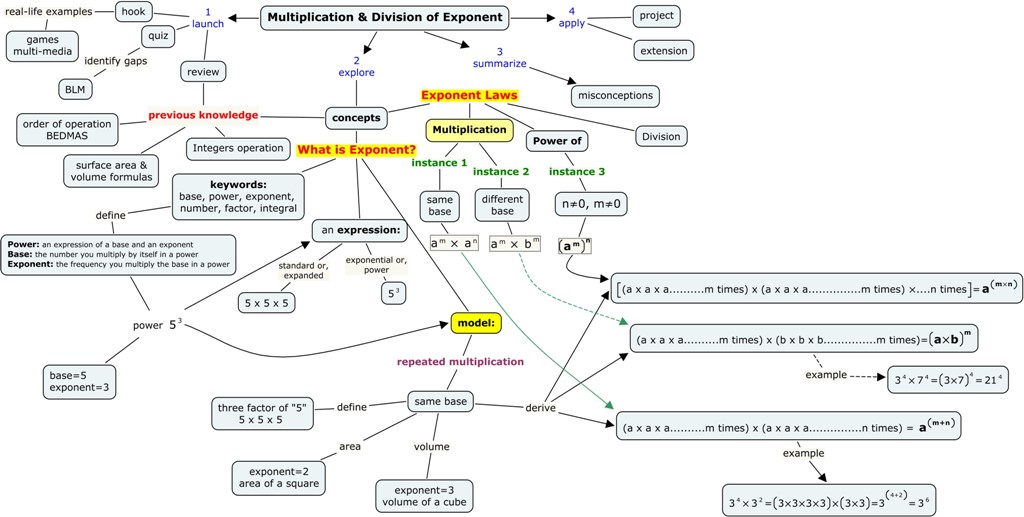
Using this model, we can derive and explain the multiplication law of exponents for powers with positive integer exponents. 
Note: This model, however, does not explain very well powers with negative integer or rational exponents (see non-instance 4).

Instance 1:Area of a 2D shape – SQUARE

This example presents the exponent laws involving multiplication of two exponents with the same, positive base as a model for understanding the area of a square. 

This square has an area A = s². Each side has the same length of s. The area is determined by multiplying the length and width of the square:

A= s¹ x s¹ = s² = s⁽¹⁺¹⁾

In this instance, the exponent laws involve the multiplication of exponents with the same base. This model can further lead into a discussion of exponents involving repeated multiplication:

a^m x aⁿ  = a^(m+n)

            ^{= (a x a x a x a........... m times) x (a x a x a x a x a............ n times)}

            ^{= a(m+n) , where a is a real number and m and n are positive integers}

^{i.e. 3⁴ x 3³ = (3 x 3 x 3 x 3) x (3 x 3 x 3) = 3⁷ = 3⁽³⁺⁴⁾} 

The formula for area of a square shape (side of length “s”) is a special case of a “power” with a base of “s” and an exponent of “2.” 

Instance 2:Volume of a 3D object – CUBE

We can also look at the volume of a cube:

V = l x w x h

For a cube, l = w = h

Therefore V = s³ = s¹ x s¹ x s¹ = s⁽¹⁺¹⁺¹⁾

or V = area of a square (or one face of a cube) x the height of the cube

V= s² x s = s⁽²⁺¹⁾ = s³

The formula for volume of a cube (side of length “s”) is a special case of a “power” with a base of “s” and an exponent of “3.”

But what if the bases of the exponents being multiplied are different?

In the case of the area of a rectangle, the formula is A = l x w, where the length and width are not the same (as they are for a square). In this case we do not add the exponents of l and w. This concept can also be applied to the volume of a rectangular prism, where the length, width and height are not the same.

The model involving the square and the rectangle can create a better understanding of the concept that the bases of numbers with exponents need to be the same in order to apply the exponent rule where the exponents are added. There can often be a misconception that any numbers with exponents can apply to this rule and this can be further disproved through more examples, i.e.:

Instance 3:Different Bases

2³ x 3² = (2 x 2 x 2) x (3 x 3) = 8 x 9 = 72 (neither 2 nor 3 can be a possible base for 72).

But try it anyways:

2⁽²⁺³⁾ = 2⁵ = 32
3⁽²⁺³⁾ = 3⁵ = 243 

Note: Neither a base of 2 nor 3 with an exponent of 5 is equal to 72, so the exponent rule does not apply to different bases 

This can also be further used to demonstrate the formula for the area and volume of a rectangle/rectangular prism, which also has different bases and therefore is an exception to this particular exponent law.
Instance 3a: Different bases; Bases with a LCF (lowest common factor)
2³ x 4² = 2³ x (2 x 2)2 = 2³ x (22 x 22)
                               = (2 x 2 x 2) x (2 x 2 x 2 x 2) = 2(3+4) = 128
Instance 3b: Different bases; Bases with a LCF (lowest common factor) and a coefficient
2³ x 6² = 2³ x (3 x 2)2 = 2³ x (32 x 22)
                               = (2 x 2 x 2) x (3 x 3 x 2 x 2) = 2(3+2) x 9 = 32 x 9 = 288

Non-Instance 1:Negative exponents

If the exponent n is a negative integer, the model of repeated multiplication does not make sense. For example, 

3^-3 might read as “multiply three by itself [for] negative three times!”

However, we can explain [negative exponents] using a model of repeated division: